Математика 5 класс контрольные работы Крайнева ФГОС — страницы 28, 29

Номер 1.
Найдите значение выражения:
а) (2³ + 3² + 4²) : 11 = (8 + 9 + 16) : 11 = 33 : 11 = 3
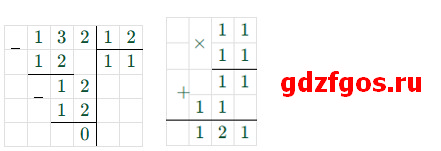
б) 132 : 12 · 11 = 11 · 11 = 121

Номер 2.
Длина прямоугольника равна 10 см, а ширина – в 2 раза меньше. Найдите площадь прямоугольника.
S = a · b
1) 10 : 2 = 5 (см) – ширина прямоугольника
2) S = 10 · 5 = 50 (см²) — площадь прямоугольника
Ответ: 50 см².

Номер 3.
Найдите объём прямоугольного параллелепипеда, если одно измерение у него равно 2 м, другое – в 3 раза больше первого, а третье равно 5 м.
V = a · b · c
1) 2 · 3 = 6 (м) — второе измерение
2) V = 2 · 6 · 5 = 60 (м³) — объём прямоугольного параллелепипеда
Ответ: 60 м³.

Номер 4.
Используя формулу пути S = ϑ · t, найдите:
а) путь, пройденный машиной за 5 ч со скоростью 65 км / ч;
S = ϑ · t
ϑ = 65 км/ч
t = 5 ч
S = 65 · 5 = 325 (км)
Ответ: путь, пройденный машиной, равен 325 км.

б) скорость автобуса, если за 4 ч он проехал 240 км;
ϑ = S : t
S = 240 км
t = 4ч
ϑ = 240 : 4 = 60 (км/ч)
Ответ: скорость автобуса равна 60 км/ч.

в) время, за которое катер прошёл 90 км со скоростью 15 км/ч.
t = S : ϑ
S = 90км
ϑ = 15 км/ч
t = 90 : 15 = 6 (ч)
Ответ: за 6 ч.

Номер 5*.
Решите задачу:
Ребро куба равно 4 дм. Найдите:
а) объём куба;
V = a · b · c
V = a³
V = 4³ = 4 · 4 · 4 = 64 (дм³)

б) площадь поверхности куба.
Sпов. = 6 · a²
S = 6 · 4² = 6 · 16 = 96 (дм²)

Ребро куба увеличили в два раза. Найдите:
в) объём;
V = 8³ = 8 · 8 · 8 = 64 · 8 = 512 (дм³)

г) площадь поверхности этого куба.
S = 6 · 8² = 6 · 64 = 384 (дм²)

Номер 1.
Найдите значение выражения:
а) (2³ + 3³ + 4²) : 17 = (8 + 27 + 16) : 17 = 51 : 17 = 3
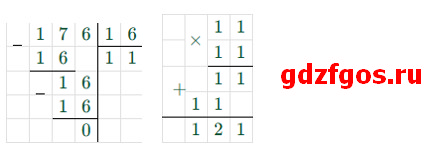
б) 176 : 16 · 11 = 11 · 11 = 121

Номер 2.
Ширина прямоугольника равна 15 дм, а длина – в 2 раза больше. Найдите площадь прямоугольника.
S = a · b
1) 15 · 2 = 30 (дм) – длина прямоугольника
2) S = 15 · 30 = 450 (дм²) — площадь прямоугольника
Ответ: 450 дм².

Номер 3.
Найдите объём прямоугольного параллелепипеда, если одно измерение у него равно 6 м, другое – в 3 раза больше, а третье равно 2 м.
V = a · b · c
1) 6 · 3 = 18 (м) — второе измерение
2) V = 6 · 18 · 2 = 12 · 18 = 216 (м³) — объём прямоугольного параллелепипеда
Ответ: 216 м³.

Номер 4.
Используя формулу пути S = ϑ · t, найдите:
а) путь, пройденный машиной за 6 ч со скоростью 80 км/ч;
S = ϑ · t
ϑ = 80 км/ч
t = 6 ч
S = 80 · 6 = 480 (км)
Ответ: путь, пройденный машиной, равен 480 км.

б) скорость автобуса, если за 12 ч он проехал 720 км;
ϑ = S : t
S = 720 км
t = 12 ч
ϑ = 720 : 12 = 60 (км/ч)
Ответ: скорость автобуса равна 60 км/ч.

в) время, за которое катер прошёл 36 км со скоростью 18 км/ч.
t = S : ϑ
S = 36 км
ϑ = 18 км/ч
t = 36 : 18 = 2 (ч)
Ответ: за 2 ч.

Номер 5*.
Решите задачу:
Ребро куба равно 8 см. Найдите:
а) объём куба;
V = a · b · c
V = a³
V = 8³ = 8 · 8 · 8 = 512 (см³)

б) площадь поверхности куба.
Sпов. = 6 · a²
S = 6 · 8² = 6 · 64 = 384 (см²)

Ребро куба уменьшили в два раза. Найдите:
в) объём;
V = 4³ = 4 · 4 · 4 = 64 (см³)

г) площадь поверхности этого куба.
S = 6 · 4² = 6 · 16 = 96 (см²)

Номер 1.
Найдите значение выражения:
а) (5³ + 13²) : 21 = (125 + 169) : 21 = 294 : 21 = 14

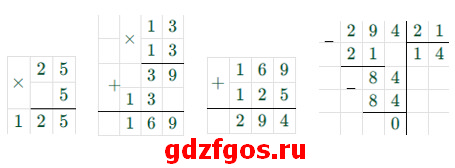
б) 132 : 11 · 12 = 12 · 12 = 144

Номер 2.
Длина прямоугольного участка земли равна 125 м, а ширина – 96 м. Найдите площадь этого участка.
S = a · b
1) S = 125 · 96 = 12 000 (м²) — площадь участка
Ответ: 12 000 м².

Номер 3.
Найдите объём прямоугольного параллелепипеда, если одно измерение у него равно 3 м, другое – в 2 раза больше, а третье равно 4 м.
V = a · b · c
1) 3 · 2 = 6 (м) – второе измерение
2) V = 3 · 6 · 4 = 18 · 4 = 72 (м³) — объём прямоугольного параллелепипеда
Ответ: 72 м³.

Номер 4.
Используя формулу пути S = ϑ · t, найдите:
а) путь, пройденный машиной за 3 ч со скоростью 80 км/ч;
S = ϑ · t
ϑ = 80 км/ч
t = 3 ч
S = 80 · 3 = 240 (км)
Ответ: путь, пройденный машиной, равен 240 км.

б) скорость мотоциклиста, если за 5 ч он проехал 475 км;
ϑ = S : t
S = 475 км
t = 5 ч
ϑ = 475 : 5 = 95 (км/ч)
Ответ: скорость автобуса равна 95 км/ч.

в) время, за которое теплоход проплыл 270 км со скоростью 45 км/ч.
t = S : ϑ
S = 270 км
ϑ = 45 км / ч
t = 270 : 45 = 6 (ч)
Ответ: за 6 ч.

Номер 5*.
Решите задачу:
Ребро куба равно 6 дм. Найдите:
а) объём куба;
V = a · b · c
V = a³
V = 6³ = 6 · 6 · 6 = 216 (дм³)

б) площадь поверхности куба.
Sпов. = 6 · a²
S = 6 · 6² = 6 · 36 = 216 (дм²)

Ребро куба уменьшили в два раза. Найдите:
в) объём;
V = 3³ = 3 · 3 · 3 = 27 (дм³)

г) площадь поверхности этого куба.
S = 6 · 3² = 6 · 9 = 54 (дм²)

Номер 1.
Найдите значение выражения:
а) (6³ + 12²) : 15 = (6 · 6 · 6 + 12 · 12) : 15 = (216 + 144) : 15 = 360 : 15 = 24

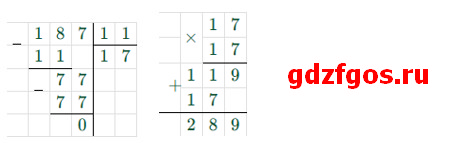
б) 187 : 11 · 17 = 17 · 17 = 289

Номер 2.
Ширина прямоугольного поля равна 375 м, а длина 1600 м. Найдите площадь поля.
S = a · b
1) 375 · 1600 = 600 000 (м²) – площадь поля
Ответ: 600 000 м².

Номер 3.
Найдите объём прямоугольного параллелепипеда, если одно измерение у него равно 6 см, другое – в 3 раза меньше, а третье равно 3 см.
V = a · b · c
1) 6 : 3 = 2 (см) – второе измерение
2) V = 6 · 2 · 3 = 12 · 3 = 36 (см³) — объём прямоугольного параллелепипеда
Ответ: 36 см³.

Номер 4.
Используя формулу пути S = ϑ · t, найдите:
а) путь, пройденный моторной лодкой за 3 ч со скоростью 18 км/ч;
S = ϑ · t
ϑ = 18 км/ч
t = 3 ч
S = 18 · 3 = 54 (км)
Ответ: путь, пройденный моторной лодкой, равен 54 км.

б) скорость автомобиля, если за 3 ч он проехал 150 км;
ϑ = S : t
S = 150 км
t = 3 ч
ϑ = 150 : 3 = 50 (км/ч)
Ответ: скорость автомобиля равен 50 км/ч.

в) время, за которое турист прошёл 24 км со скоростью 6 км/ч.
t = S : ϑ
S = 24 км
ϑ = 6 км/ч
t = 24 : 6 = 4 (ч)
Ответ: за 4 ч.

Номер 5*.
Решите задачу:
Ребро куба равно 9 см. Найдите:
а) объём куба;
V = a · b · c
V = a³
V = 9³ = 9 · 9 · 9 = 81 · 9 = 729 (см³)

б) площадь поверхности куба.
Sпов. = 6 · a²
S = 6 · 9² = 6 · 81 = 486 (см²)

Ребро куба уменьшили в три раза. Найдите:
в) объём;
V = 3³ = 3 · 3 · 3 = 27 (см³)

г) площадь поверхности этого куба.
S = 6 · 3² = 6 · 9 = 54 (см²)