
- Тип: контрольные работы ФГОС
- Авторы: Крайнева
- Год: 2024
- Издательство: Просвещение
Контрольная работа № 6 (п. 18 – 19)
Вариант 1
Номер 1.
Выпишите:
а) все делители числа 18;
1, 2, 3, 6, 9, 18.
б) все двузначные числа, кратные 19.
19, 38, 57, 76, 95.
Номер 2.
Выполните деление с остатком:
а) 63 : 25 = 2 (ост. 13)
б) 531 : 38 = 13 (ост. 37)

Номер 3.
Какие цифры можно записать вместо звёздочки в числе 783*, чтобы оно делилось:
а) на 2:
7830; 7832; 7834; 7836; 7838.
б) на 9:
7830; 7839.
Номер 4.
Решите уравнение:
| а) 5k + 11k — 2k = 112 14k = 112 k = 112 : 14 k = 8 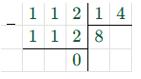 |
б) 15p — 12p + 8 = 374 3p + 8 = 374 3p = 374 — 8 3p = 366 р = 366 : 3 р = 122 |
Номер 5*.
Во сколько раз количество двузначных чисел, делящихся на 3, больше количества двузначных чисел, делящихся на 6?
Двузначные числа, делящиеся на 3: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99 (30 чисел).
Двузначные числа, делящиеся на 6: 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96 (15 чисел).
30 : 15 = 2
Ответ: в 2 раза.
Вариант 2
Номер 1.
Выпишите:
а) все делители числа 24;
1, 2, 3, 4, 6, 8, 12, 24.
б) все двузначные числа, кратные 26.
26: 26, 52, 78.
Номер 2.
Выполните деление с остатком:
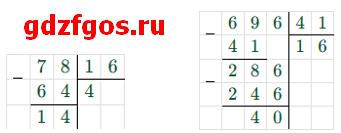
а) 78 : 16 = 4 (ост. 14)
б) 696 : 41 = 16 (ост. 40)
Номер 3.
Какие цифры можно записать вместо звёздочки в числе 347*, чтобы оно делилось:
а) на 5:
3470; 3475.
б) на 3:
3471; 3474; 3477.
Номер 4.
Решите уравнение:
| а) 6m + 13m — 7m = 108 12m = 108 m = 108 : 12 m = 9 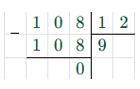 |
б) 23t — 14t — 11 = 781 9t — 11 = 781 9t = 781 + 11 9t = 792 t = 792 : 9 t = 88 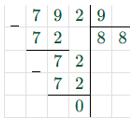 |
Номер 5*.
Во сколько раз количество двузначных чисел, делящихся на 9, меньше количества двузначных чисел, делящихся на 3?
Двузначные числа, делящиеся на 3: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99 (30 чисел).
Двузначные числа, делящиеся на 9: 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 (10 чисел).
30 : 10 = 3
Ответ: в 3 раза.
Вариант 3
Номер 1.
Выпишите:
а) все делители числа 28;
1, 2, 4, 7, 14, 28.
б) все двузначные числа, кратные 17.
17, 34, 51, 68, 85.
Номер 2.
Выполните деление с остатком:
а) 68 : 24 = 2 (ост. 20)
б) 623 : 37 = 16 (ост. 31)

Номер 3.
Какие цифры можно записать вместо звёздочки в числе 681*, чтобы оно делилось:
а) на 5:
6810; 6815.
б) на 9:
6813.
Номер 4.
Решите уравнение:
| а) 3t + 24t — 6t = 441 21t = 441 t = 441 : 21 t = 21 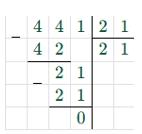 |
б) 18k – 13k + 7 = 532 5k + 7 = 532 5k = 532 — 7 5k = 525 k = 525 : 5 k = 105 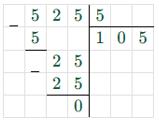 |
Номер 5*.
Во сколько раз количество двузначных чисел, делящихся на 34, больше количества двузначных чисел, делящихся на 8?
Двузначные числа, делящиеся на 34: 34; 68 (2 числа).
Двузначные числа, делящиеся на 8: 16; 24; 32; 40; 48; 56; 64; 72; 80; 88; 96 (11 чисел).
11 : 2 = 5,5
Ответ: в 5,5 раз.
Вариант 4
Номер 1.
Выпишите:
а) все делители числа 16;
1, 2, 4, 8, 16.
б) все двузначные числа, кратные 23.
23, 46, 69, 92.
Номер 2.
Выполните деление с остатком:
а) 84 : 33 = 2 (ост. 18)
б) 886 : 38 = 23 (ост. 12)

Номер 3.
Какие цифры можно записать вместо звёздочки в числе 497*, чтобы оно делилось:
а) на 3:
4971, 4974, 4977.
б) на 10:
4970.
Номер 4.
Решите уравнение:
| а) 7t + 15t — 4t = 126 18t = 126 t = 126 : 18 t = 7 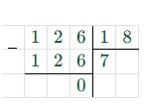 |
б) 28t — 16t — 9 = 843 12t — 9 = 843 12t = 843 + 9 12t = 852 t = 852 : 12 t = 71 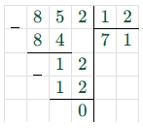 |
Номер 5*.
Во сколько раз количество трёхзначных чисел, делящихся на 9, меньше количества трёхзначных чисел, делящихся на 3?
Первым целым трёхзначным числом, которое делится без остатка на 3 будет число 102, а последнее – 999. Всего трёхзначных чисел 900. Каждое третье из них будет делиться на 3 без остатка. Получается, 900 : 3 = 300 целых трёхзначных чисел, кратных 3.
Первым трёхзначным числом, которое делится без остатка на 9 будет 108, а последнее – 999. Всего трёхзначных чисел 900. Каждое девятое из них будет делиться на 9 без остатка. Получается, 900 : 9 = 100 целых трёхзначных чисел, кратных 9.
300 : 100 = 3
Ответ: в 3 раза.

