- Тип: учебник ФГОС часть 1
- Авторы: Моро, Бантова, Бельтюкова
- Год: 2023
- Серия: Школа России
- Издательство: Просвещение
Номер 1.
Прочитай записи.
Найди значения этих выражений.
К числу 9 прибавить число 7:
9 + 7 = 16
Из числа 23 вычесть число 3:
23 — 3 = 20
К числу 30 прибавить число 6, затем прибавить число 1:
30 + 6 + 1 = 37
Из числа 15 вычесть число 7, затем прибавить число 3:
15 — 7 + 3 = 11
Из числа 18 вычесть сумму чисел 4 и 6:
18 — (4 + 6) = 8
Из числа 25 вычесть разность чисел 15 и 10:
25 — (15 — 10) = 20
Номер 2.
Запиши выражения и найди их значения.
1) Из числа 16 вычесть разность чисел 9 и 7.
16 — (9 — 7) = 16 — 2 = 14
2) К числу 10 прибавить разность чисел 7 и 5.
10 + (7 — 5) = 10 + 2 = 12
Номер 3.
Используя числа 10, 9, 1 знаки «+», «−» и скобки, составь различные выражения и найди их значения.
(9 + 1) – 10 = 0
10 — (9 — 1) = 2
(10 + 9) – 1 = 18
(10 — 9) + 1 = 2
(9 – 1) + 10 = 18
Номер 4.
В мастерской было на ремонте 6 машин. Через день поставили на ремонт еще 3 машины, а 2 машины вернули после ремонта. Сколько машин стало в мастерской?
1) Выбери выражение, которое составлено по этой задаче, и реши задачу.
| 6 — 3 + 2 | 6 + 3 + 2 | 6 + 3 — 2 | 6 — 3 — 2 |
6 + 3 – 2 = 7 (м.) – стало в мастерской
Ответ: 7 машин.
2) Изменяй условие задачи так, чтобы для решения подходили другие из написанных выражений. Реши новые задачи.
1) В мастерской было на ремонте 6 машин. Через день вернули владельцам после ремонта 3 машины, а ещё 2 машины поставили на ремонт. Сколько машин стало в мастерской?
6 — 3 + 2 = 5 (м.)
Ответ: 5 машин.
2) В мастерской было на ремонте 6 машин. Утром взяли в ремонт ещё 3 машины, а вечером ещё 2. Сколько машин стало в мастерской?
6 + 3 + 2 = 11 (м.)
Ответ: 11 машин.
3) В мастерской было на ремонте 6 машин. Утром владельцам вернули после ремонта 3 машины, а вечером ещё 2. Сколько машин осталось в мастерской?
6 — 3 — 2 = 1 (м.)
Ответ: 1 машина.
Номер 5.
| 12 мм > 1 см (1 см = 10 мм) 9 см < 1 дм (1 дм = 10 см) |
56 мин < 1 ч (1 ч = 60 мин) 1 ч < 100 мин (1 ч = 60 мин) |
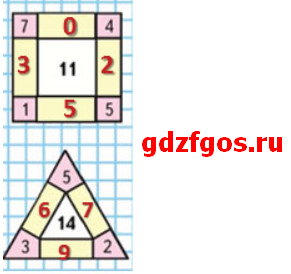
Номер 6.
В занимательных рамках сумма чисел, расположенных по каждой стороне фигуры, должна быть равна числу в центре фигуры.